Construction of a Tabletop Michelson Interferometer
Abstract
All atoms are made up of protons and neutrons, which are in turn comprised of quarks. The particles “gluing” the quarks together are known as gluons. The interaction of quarks and gluons is still not entirely understood, specifically how they are confined in the nucleus such that lone quarks are never seen. The nuclear physics group at the University of Connecticut is part of the GlueX Experiment, which hopes to probe directly the gluon bond and understand its mechanical properties. The probe used by GlueX is a high energy (small wavelength), polarized photon (particle of light) generated by a technique known as coherent bremsstrahlung . This technique involves radiation of photons as a high energy electron beam passes through a carefully oriented diamond wafer. Because of the potential for contamination, it is necessary to suspend the diamond wafer rather than mount on a ridged mount. The diamond is currently suspended on thin tungsten wires. Proper orientation ensures a high degree of polarization, which requires stable mounting of the diamond. The goal of my research is to investigate the mechanical properties of the mount and eliminate the possibility of vibration of the crystal.
The pupose of this page is to describe the work being done on the development of a system to analyze these vibrations. Two different techniques will be used to determine the amplitude and frequency of these vibrations. First, a direct imaging technique will be used. A Michelson interferometer will also be constructed, and will be used in not only the vibrational research, but also in the analysis of the diamond surface structure.
Construction
Parts List
The following is a lis of the parts used in the construction of the inerferometer, along with a brief descripton of the parts.
| Category | Item | Description |
| Beam Splitter | Beam Splitter Cube | (2cm)3, AR, 400-700nm |
| Kinematic Platform Mount | (2in)2 | |
| Prism Clamp | Large clamping arm | |
| Camera | Casio Ex-F1 | |
| Mirrors | Protected Silver Mirror | 25.4mm Dia., R≈98% |
| Mirror Holder | Standard 1" holder | |
| Kinematic Mirror Mount | Adjustable Kinematic mount for 1" holder | |
| Light Source | 532nm Green laser Module | 5mW, 5mm spot size, <1.4 mrad div. |
| Kinematic V-Mount | Small Mount with Attached Clamping Arm | |
| Beam Expander/Spatial Filter | Pinhole | 5μm, 10μm, 15μm, and 20μm pinholes |
| Pinhole Holder | 1/2" and 1" standard holder | |
| Small Plano-Convex Lens | f=50mm, 12.7mm Dia., AR coating | |
| Lens Holders | Holder for 1/2" and 1" optics lenses | |
| Large Plano-Convex Lens | f=150mm, 25.4mm Dia., AR coating | |
| Translation Stages | Small Linear Translation Stage | 1 dimension translation stage |
| 3-Axis Linear Translation Stage | 3 dimension translation stage | |
| Common Mechanics | Posts | 3/4" and 1" high posts, 1/2" Dia. |
| Post Holders | 1" high post holders | |
| Safety Equipment | Laser Safety Glasses | Green and Blue laser beam protection |
Estimating Camera Sensitivity
Originally the parts list called for a 1mW laser. There was a concern, however, that this laser would not be powerful enough to produce interferograms. It is critical to understand the sensitivity of the camera to light from the interferometer, given the high intended image acquisition speed. The camera purchased for this setup, Casio EX-F1, has a movie frame rate capability of 1200 Hz. The following information allows an order of magnitude estimate of the sensitivity. (The camera uses a CMOS sensor. Note that lx=lm·m2)
- a sample CMOS chip, Micron's MT9P401, has sensitivity of 1.4 V/lx·s and supply voltage of 2.8 V yielding 2 lx·s of light energy to saturation.
- Light intensity conversion - 320 lm/W given:
- a 100 W incandescent light bulb is measured to have the perceived intensity of about 1600 lm
- a rough figure of efficiency for a 100 W is 5%
Using these conversions, the sensor pixels saturate at 6.3×10-3 W·m2·s. At 1200 Hz acquisition rate, assuming 100% duty cycle, the saturation figure is 5.2×10-6 W·m.
Now, let us assume that only about 5% of 1 mW laser light reaches the sensor due to cleanup in the beam expander and the light transmitted through the diamond. If the light is expanded to a 2 cm diameter beam, the beam at the sensor is rated at 1.6×10-8 W·m2
The two order of magnitude shortfall means that very little of the dynamic range of the sensor will be used, leading to a low signal to noise ratio. For this reason, a 5mW laser was chosen over a 1mW.
Choosing a pinhole
It is crucial that any spherical aberration are removed by way of pinhole. The laser spot is passed through a pinhole, which acts to expand the beam. This expansion creates a patter known as an Airy pattern[ http://en.wikipedia.org/wiki/Airy_disk].
Camera Calibration
Analysis of videos taken of the vibration of the diamond wafer can lead to information about both the frequency and the amplitude of vibration. To perform simultaneous measurements of both parameters, a precise camera calibration was necessary.
Video Analysis
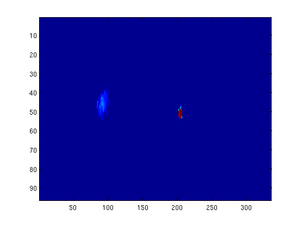
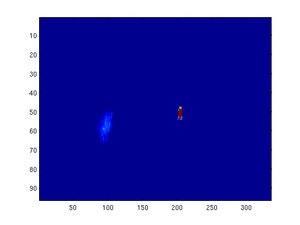
Originally, it was our intention to perform interferometry to analyze the diamond vibration. After several attempts to use the interferometer, it was determined that the vibration amplitude was simply too high to perform interferometry. Instead, a direct imaging technique was used to analyze the diamond vibration. An interesting phenomenon occurred when the direct imaging device was used. The reflected spot entering the camera lens created an artifact known as a lens flare. Typically lens flares are undesirable, but in our case, the lens flare movement directly correlated to the movement of the reflected beam spot on the lens surface. By careful calibration, the pixel movement on the image versus the angular displacement of the diamond surface was determined.
Calibration Set-Up
The following is an image of the device used for the camera calibration:
IMAGE OF CALIBRATION DEVICE
This calibration device was used to determine the change in pixel location of the center of the lens flares based on angular displacement. To do this, the camera was mounted horizontally on a 1.40m long bar. The camera end was free to rotate about a pivot located at the opposite end of the rod, above which a mirror was mounted. A linear micro-adjustment translation stage was placed below the camera end.
Image Analysis
A high-speed (1200fps)video of the movement of the flare spot was then taken and analyzed using a fitting program. of the large number of images, a batching process was developed to aid in the video analysis. First, a built in Linux program, ffmpeg, separates the video into individual frames. Next, a program was developed to determine the center of th flare spot for each image. To find the location of the center of the flare, several lines of code were implemented:
This program imports images with the name beginning with fnameref, starting with fnameref-initial.bmp . The program then converts the image into a matrix of intensity values and separates out the green channel. The plot for this channel is then images in flase color, with intensity ranging from low (blue) to high (red). The bright center spot is the point-to-point image of the illuminated diamond wafer. This spot remains fixed (the diamond is not really moving in space, simply rotating about fixed axes). Since this bright spot is many times brighter than the flair spot we are trying to investigate, we artificially mast this location out, so that the fit does not consider those points.
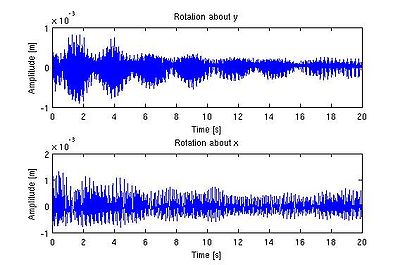
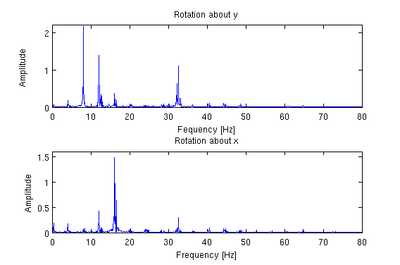
The program then fits the intensity value to a Gaussian (called as gauss2(n,m,par)) and uses this fit to find the center of the image flare. Since it is possible for the flare spot to be located outside the frame of the image, several checks are performed to ensure that the location which the program concludes is plausible. If not, the program notes the check failure in a vector known as badvec (originally a vector of all 1’s) by placing a 0 at the cell corresponding to number of the failed fit. The Gaussian program then fits the actual intensity to the fit intensity at each pixel. Suitable shape and amplitude parameters for the flare spots were chosen based on analysis of individual images. Once the fit is complete, the program put the x and y location for an image in a matrix called pars, with the x location in column 1 and the y locations in column 2. The program loops this fitting procedure until all the images have been fit. Once the fit is complete, the mean value for the x and y positions are subtracted from their respective columns and the data points are scaled (using the data received from the camera calibration) to obtain the deflection of the glass from center. We can also find the frequency components of this vibration by taking the Fourier transform of the amplitude plot.