Hybrid Photodiode

A Hybrid Photodiode from DEP was used as a photo-intensity reference for most light tests in the lab. It particular it served to calibrate the detection efficiencies of the candidate Silicon Photomultipliers (SiPMs) for the Tagger Microscope.

HPD Photo-cathode efficiency as a function of wavelength.

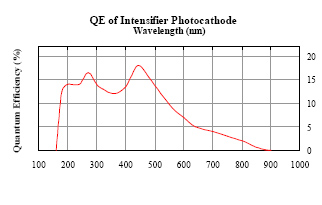
The quantum efficiency of this device is shown in the adjacent figure. The DEP-supplied device provides a gain factor of 2700 at the HV of 12 kV and additionally requires 40 - 80 V bias to collect the electrons across the diode junction. Built into the package is a transimpedance amplifier with 50 kΩ || 1.5 pF feedback, requiring ±5 V supplies. The amplifier circuit also contains a 51.1 Ω resistor in series with the output. Reading out the HPD signal from the amplifier with 50 Ω termination creates a about a factor of two (50 Ω/(50 Ω + 51.1 Ω)) on top of the 50 kΩ current to voltage conversion.

Frequency Response

Based on the circuit described above, a two-pole response model was developed of the form:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \tilde{V}_{out}(\omega)=\frac{\alpha}{a\omega^2+ib\omega+c}\tilde{I}_{in}(\omega)}

where the parameters in the gain pre-factor (g(ω)) are:

• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha = -G/C_F}
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle a = -(1+C_{HPD}/C_F)}
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle b = G + 1/(R_F C_F)}
• Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c = G/(R_F C_F)}

The subscript 'F' in the above expressions stands for op-amp feedback components. G is the gain-bandwidth product - nominally 1.6 GHz but was adjusted to 21 GHz to produce physical results. (Applying this response to the measured responses of LED pulses with the narrow nominal bandwidth produced negative LED intensities!)

The HPD response in the time domain is a straightforward inverse Fourier Transform:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(t)=\int\limits_{-\infty}^{\infty}\frac{\alpha}{a\omega^2+ib\omega+c}\, e^{i\omega t}\, d\omega = \int\limits_{-\infty}^{\infty}\frac{\alpha}{(\omega-\omega_+)(\omega-\omega_-)}\, e^{i\omega t}\, d\omega}

where     Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \omega_\pm = \frac{-ib}{2a} \pm \frac{ \sqrt{-b^2-4ac} }{2a} = \omega_1 \pm i\omega_2}

Thus, in the complex space, this integral is equivalent to the residues of two poles. Depending on the constants provided, the poles are situated either on the positive imaginary axis or along the -ib/2a line. For the physical constant of our circuit, the former set of poles is relevant. The resulting response function is:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle g(t) = \frac{2\pi\alpha}{\omega_2} e^{i\omega_1 t} \sinh \omega_2 t }

Since the response seen on the HPD circuit output is the convolution of the light pulse shape (f_L) with the response function of the HPD, the pulse shape can be recovered by deconvolving the measured signal (f_M) with the g(ω). By the convolution theorem:

Failed to parse (MathML with SVG or PNG fallback (recommended for modern browsers and accessibility tools): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f_L(t) = \mathcal{F}^{-1} \left\{ \frac{f_M(\omega)}{g(\omega)} \right\} }

This is a delicate procedure, in practice, as the division is sensitive to the small high-frequency errors. Direct application of this results in very noisy results. A good remedy is a low-pass filter on the spectrum of the measured signal (taking care to preserve the shape of the signal by keeping the cutoff well above the highest relevant frequencies).

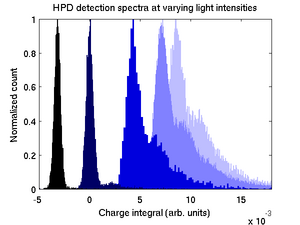
Modeling the HPD spectrum

The HPD spectra collected from large pulses should essentially be a convolution of the Poisson distribution, in the limit of high mean count, with the electronic noise function, which is known to be broad enough to make individual photon peaks impossible to resolve. Both of these functions are Gaussian and the result should be a Gaussian as well. The measured spectra show a peculiar deviation (shown on the right.)